Thermal Resistivity and Thermal Conductivity

Thermal conductivity of a pure element or a stoichiometric phase at temperature above 273 K is described as a function of temperature using the following equation:

k= A + B T + C T-1 + D T2

(1)

where k is the thermal conductivity and T is the temperature in Kelvin. This function can reasonably fit most of the experimental thermal conductivity data of elements at temperature above 273 K.

The thermal conductivity of a solid solution phase can be calculated from thermal resistivity, which is the reciprocal of thermal conductivity. According to the Nordheim rule, the thermal resistivity ( ρ ) of a solid solution phase can be described by the following Redich–Kister polynomials:

(2)

where is the thermal resistivity of the a solution phase in the A-B system. x_j and r_j are the mole fraction and thermal resistivity of pure elements j, respectively. L_i are the ith order interaction parameters which are used to describe the effect of solute elements on the thermal resistivity. In general, the interaction parameter can be expressed as:

(3)

where the parameters a_i, b_i and c_i are evaluated based on the experimental data.

In real alloys, multiple phases coexist, influencing the overall thermal conductivity. The thermal conductivity is affected by the volume fraction and morphology of these phases. The series and parallel models are fundamental theoretical approaches for two-phase composites, representing phase arrangements perpendicular and parallel to the heat flow direction, respectively. These models establish the lower and upper bounds of the effective thermal conductivity, expressed as:

(4)

(5)

where κ_s and κ_p represent the effective thermal conductivities of an alloy with two-phase microstructure under series and parallel model, and v₁, v₂, κ₁ and κ₂ represent volume fractions and thermal conductivities of the two phases, respectively.

Pandat provides System_Property definition to automatically calculate a system property based on a multi-phase structure. The thermal conductivities of an alloy with multiphase microstructure under series model and parallel model can be formulated as

(6)

(7)

where fi, and κ_i represent molar fraction and thermal conductivity of the phase i, respectively.

Helsing et al. [1991Hel] proposed the effective thermal conductivity of lamellar eutectic microstructure relates to series and parallel models.

(8)

And the effective thermal conductivity of an alloy with multiphase microstructure can be calculated using Eq. 6-Eq. 8.

In this example, thermal resistivity of the Al-Mg binary alloys is described using the User-Defined Property function.

As shown in the AlMg_ThCond.tdb, the thermal resistivity ThRss property is first defined as User-Defined Property.

Type_Definition z PHASE_PROPERTY ThRss 1 !

As is seen, the thermal resistivity of the Fcc phase or the Hcp phase follows the same format as that of Gibbs energy for a disordered solution phase.

Thermal resistivity of the intermetallic phases with narrow solid solubility rage in the phase diagrams is treated like that of a stoichiometric compound phase, i.e., it is composition independent and is described as below:

In order to describe thermal resistivity within multi-phase region, the system properties using different models (Series and Parallel), are then defined by the following commands:

System_Property Sys_ThRss_S 1 !

System_Property Sys_ThRss_P -1 !

PROPERTY Sys_ThCond_S 298.15 1/Sys_ThRss_S; 6000 N !

PROPERTY Sys_ThCond_P 298.15 1/Sys_ThRss_P; 6000 N !

PROPERTY Sys_ThCond 298.15 0.25*(Sys_ThCond_P+sqrt(Sys_ThCond_P*Sys_ThCond_P +8*Sys_ThCond_P*Sys_ThCond_S)); 6000 N !

PROPERTY Sys_ThRss 298.15 1/Sys_ThCond; 6000 N !

After the thermal resistivity has been properly modeled for each phase, the thermal conductivity of each phase and that of the system can be directly calculated and outputed by using extra output in Pandat defined as 1/ThRss(@*) and 1/Sys_ThRss, respectively.

Pandat also provides a Solidification Property function to calculate the thermal conductivity of an alloy under three different cooling/heat-treated conditions. As Cast (Scheil) assumes that the alloy solidifies from liquid under Scheil condition with no diffusion in solid at any temperature, which results in a typical as-cast microstructure. Equilibrium (Lever) assumes that the alloy reaches equilibrium at any temperature like lever rule condition in solidification. Quench assumes that the alloy reaches equilibrium at the given temperature and keeps the microstructure unchanged to lower temperature, which corresponds to the microstructure of an alloy being aged for infinite time. These three functions give the user flexibilities to calculate the effective thermal conductivity of an alloy with the microstructure formed through different solidification / heat-treatment conditions.

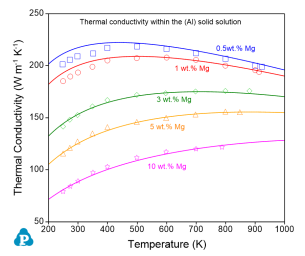
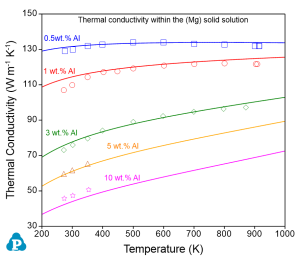
The comparisons between the calculated and measured thermal conductivities of the Al-Mg alloys are shown in Figure 1 . This example demonstrates that the User-Defined Property function is very powerful and flexible to allow users define various types of properties. The property can be a function of any phase properties that can be calculated by PanPhaseDiagram module.